Accurately estimating a size and a pose of a real world box in a cluttered environment is a common problem in logistics automation, yet there is no well accepted solution that performs well under different scenarios.
Problem statement: Given a point cloud (i.e. a set of points in 3D) belonging to a single real world box, compute a cuboid that best fits the point cloud and provides the best estimate of the real world box.
Challenges:
- the algorithm should be robust to various outliers: camera noise, segmentation issues
- point cloud may contain points from neighboring boxes
- occasionally, point cloud may contain multiple boxes due to segmentation issues
- many boxes will have some form of occlusion from neighboring boxes and objects
For the sake of brevity, this post will focus on a single camera scenario, but the solution can be further extended to support multiple cameras.
Short description:
Under the single camera assumption, each box will have one, two or at most three surfaces visible on the RGB-D data. Hence, this plane fitting algorithm is based on fitting each of those visible surfaces, one surface at a time. It is the extension of the “vanilla” single plane RANSAC to fit up to 3 mutually orthogonal planes.
Depending on the number of visible surfaces, plane fits will have one of the following forms:
- single full plane
- two mutually orthogonal half planes, intersecting at a line
- three mutually orthogonal quarter planes, intersecting at a point



! Fitting surfaces of the box in the above mentioned manner allows the cuboid fit to be robust to various outliers. In particular, it is robust to any outlier that does not lie on the surface of a fit.
Algo steps
Single plane fit
Randomly sample 3 unique points from the point cloud to compute a plane that is uniquely defined and passes through 3 points.
Set the direction of the plane normal to point towards “inside” of the box. Under the single camera assumption, this is trivially set by keeping angle between plane normal and vector – tracing the ray out coming from the camera, under 90 degrees (see fig 2 left).
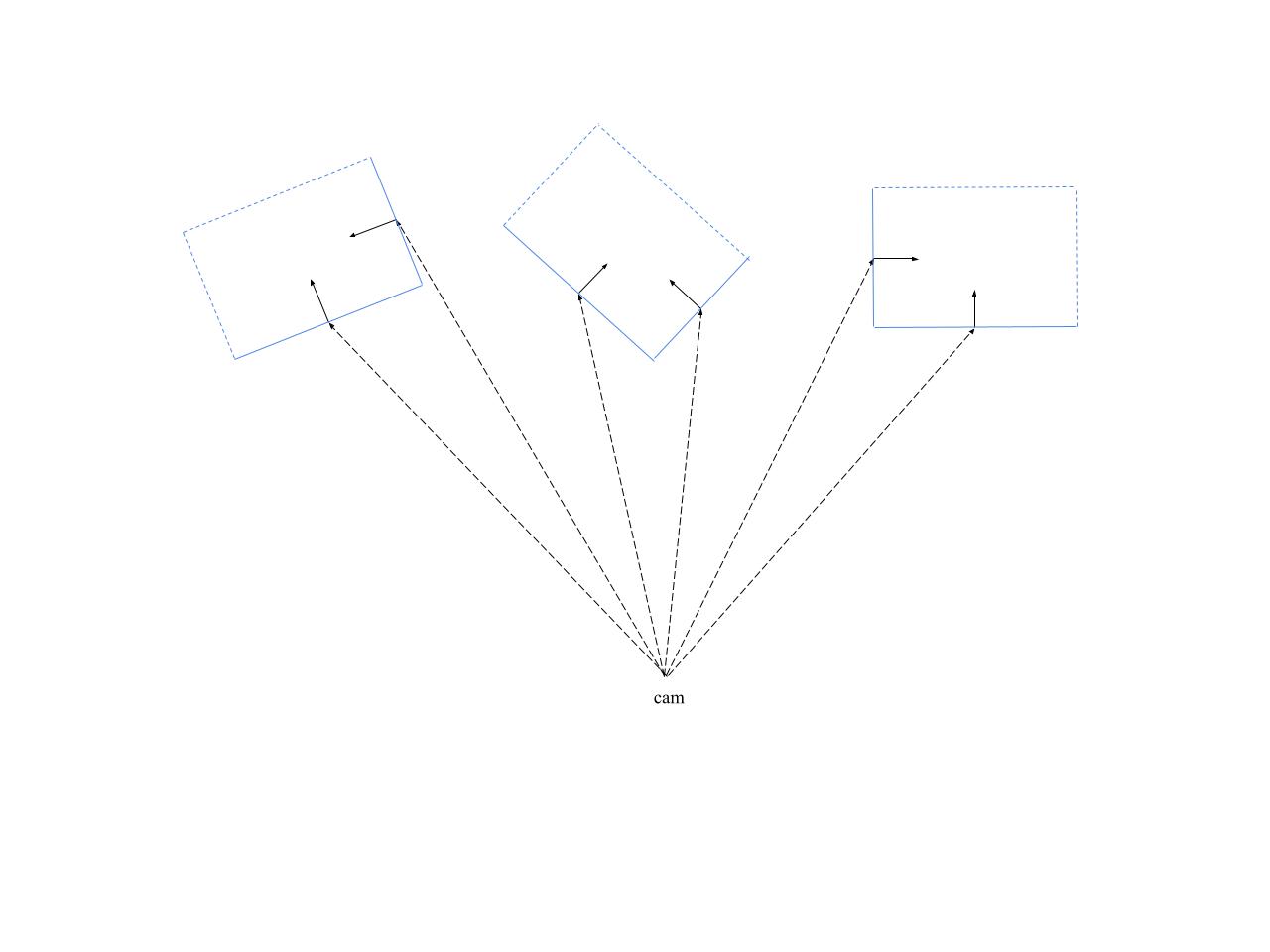
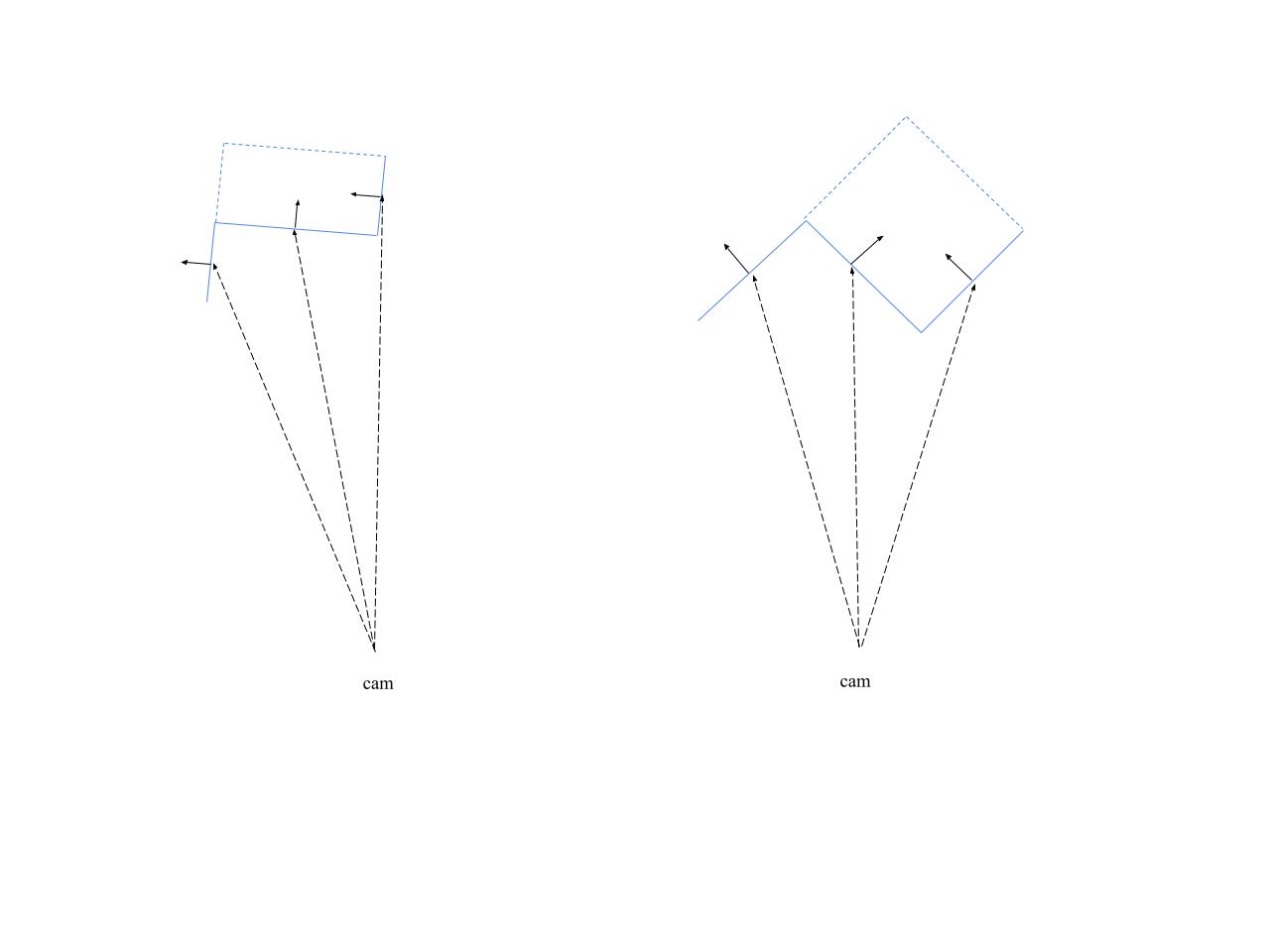
This simple assumption about plane normal is a key. Since no point should lie outside the box, any points in the negative direction of normal can be safely excluded, making the fit robust to points from neighboring boxes in a cluttered scene (see fig 2 right).
Given a plane, compute the following:
- inliers (red): points within [neg, pos] distance from the plane, considered to belong to the plane
- positive outliers (blue): residual points on the direction of the normal. If enough of them left, continue to the next step to fit another orthogonal plane
- negative outliers (grey): can be ignored

Double half plane fit
Randomly sample 2 points from the residual point cloud to compute a plane orthogonal to plane #1.
- Set the direction of normal to point towards “inside” the box
- Compute inliers and positive outliers of the plane
Each fitted plane cuts other planes in half.
- Update plane #1 to only keep inliers that are also either inliers or positive outliers of plane #2. Update plane #2, respectively.
- Compute residual cloud: positive outliers of both planes. If enough, continue to the next step.

Triple quarter plane fit
Randomly sample a single point from the residual cloud and compute a plane orthogonal to planes #1 and #2.
- Set the normal, compute inliers and positive outliers.
- Again, each plane cuts other planes into half. Convert the fit into quarter plane fits.
Some additional details not discussed on this post:
- Sequential vs Parallel fits
- Optimized search: fit plane for N iterations, choose top K fits. For each fit, fit next plane for N/K iterations
- Goodness of fit: #inliers – W * l2_distance
- Single plane fit: second normal estimation