Depth Estimation/Completion for Transparent and Reflective Objects

Reflective and transparent objects pose a common issue for depth cameras. This project describes my experiments with one of the state-of-the-art depth estimation/completion solutions.

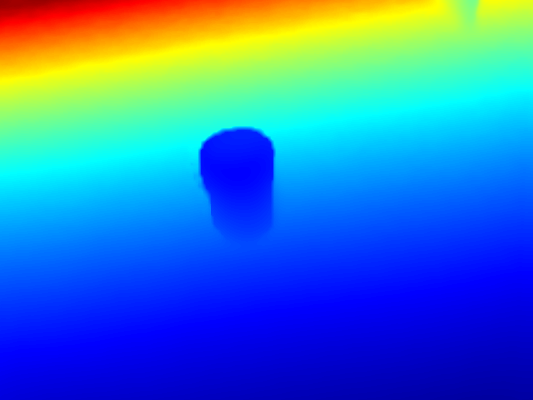
Given an RGB-D image (fig 1), use deep convolutional networks followed by a global optimization algorithm to predict the missing and erroneous depth information.

Start by using only the color image to predict the following set of images:

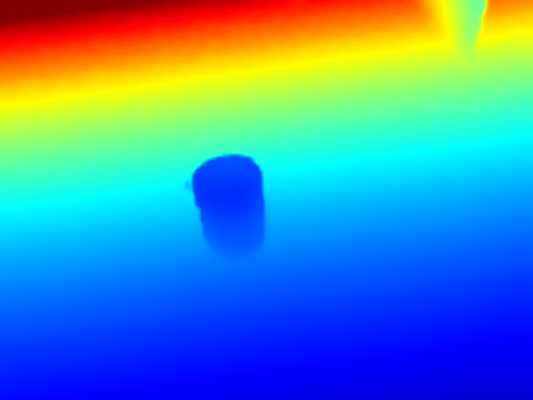
Segmentation mask: the original depth image has erroneous values for pixels corresponding to transparent/reflective objects that are unreliable. We use a deep convolutional semantic segmentation network (Deeplabv3+ with DRN-D-54 backbone) to predict a binary mask of transparent/reflective objects from a color image, and use the mask to remove all unreliable pixels from the original depth. (See fig 2 for mask and intermediate depth)
Surface normals: by providing a color image as an input to a deep convolutional network, predict pixel-wise surface normals. Again the same architecture Deeplabv3+ with DRN-D-54 is used, the last convolutional layer is modified to have 3 output classes. Output is l2 normalized to make sure the estimated normals are unit vectors (See fig 2, surface normals).
Boundary detection: use Deeplabv3+ with DRN-D-54 to predict occlusion boundaries. Given a color image, the network classifies each pixel of the input image into one of the following categories: (1) non-edge, (2) depth discontinuity, and (3) contact edge (See fig 2, occlusion boundaries). Since the ratio of boundaries to background is low, weighted cross-entropy entropy loss is used.

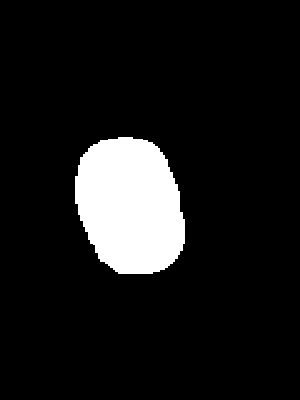
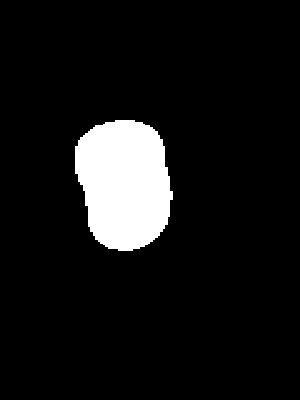
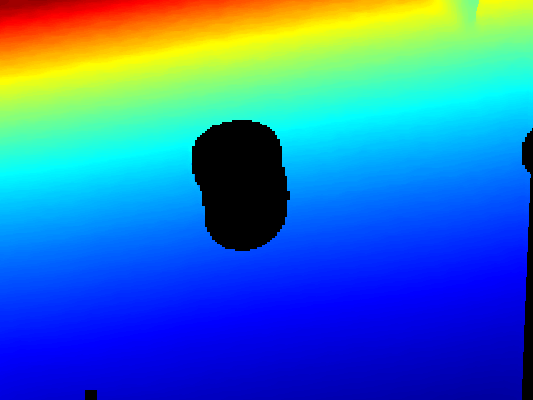
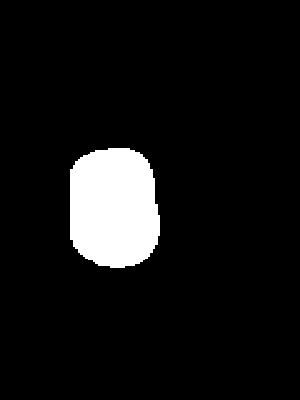
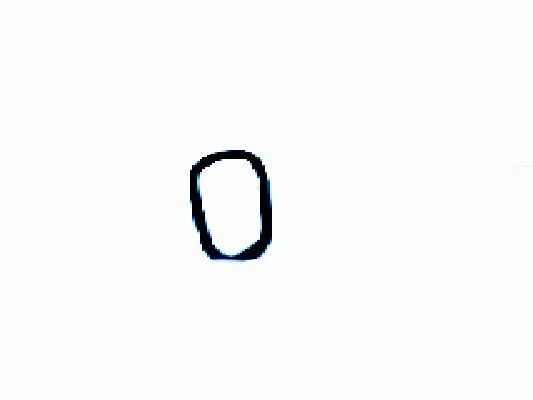
fig 2: mask, surface normals, occlusion boundaries and intermediate depth

Global optimization for depth: given predicted surface normals, occlusion boundaries and intermediate depth with “bad” pixels removed, the final step is to compute the missing depth via a global optimization algorithm. In particular, the following weighted sum of squared errors is minimized: E = λ_d * E_d + λ_s * E_s + λ_n * E_n * B, where E_d is the distance between the estimated depth and the original depth, E_s measures the difference in depth of neighboring pixels, and E_n measures the consistence between estimated depth and predicted surface normals.